ROS2 TF2

Introduction

This tutorial explains static and dynamic transforms. ROS is using the package tf2_ros as an easy accessible and intuitive API to describe the relationship between coordinate frames. The online documentation can be found at http://wiki.ros.org/tf2.

• Lines beginning with $ are terminal commands.

  • To open a new terminal → use the shortcut Ctrl + Alt + T.

  • To open a new tab inside an existing terminal → use the shortcut Ctrl + Shift +T.

  • To kill a process in a terminal → use the shortcut Ctrl + C.

• Lines beginning with # indicate the syntax of the commands.

• Code is separated in boxes.

• Code is case sensitive.

Creating a Static Transform

A static transform is an invariant coordinate transformation and describes the relationship between two frames. A definition can be done through launch files by using the static_transform_publisher node, which contains a publisher to the /tf_static topic. Provide the following arguments to describe the relationship between a parent and a child frame:

Arguments: x y z yaw pitch roll parent_frame child_frame

The translation is in meters. The rotation is denoted as Euler angles in radians or in quaternion values as shown in the alternative below:

Arguments: x y z qx qy qz qw parent_frame child_frame

Create a new package myrobottf in your robot_ws workspace. Now create a launch file turtlebot3_tf.launch.py in this package. Use the given example as a skeleton (Euler angle syntax):

Listing 13 simple static tf broadcaster launch file

#!/usr/bin/env python3

from launch import LaunchDescription
from launch_ros.actions import Node

def generate_launch_description():
    return LaunchDescription([
        Node(
            package='tf2_ros',
            node_executable='static_transform_publisher',
            node_name='parent_to_child_tf',
            arguments=['0.0', '0.0', '0.25', '3.14159', '0.0', '0.0', 'my_parent_frame', 'my_child_frame'],
            output='screen'),
    ])

Create the transformation tree of the turtlebot3 by starting multiple running processes of the node static_transform_publisher. Take care to name them differently:

→ Relationship between the frames base_footprint and my_base_link:

• Translation, t = (x, y, z)´ = (-1.0, 0, 0.01)´

• Rotation, r = (roll, pitch, yaw)´ = (0, 0, 0)´

→ Relationship between the frames my_base_link and my_camera_rgb_optical_frame:

• Translation, t = (x, y, z)´ = (0.015, 0.0913, 0.0945)´

• Rotation, r = (roll, pitch, yaw)´ = (0, 0, 0)´

→ Relationship between the frames my_base_link and my_imu_link:

• Translation, t = (x, y, z)´ = (0, 0, 0.068)´

• Rotation, r = (roll, pitch, yaw)´ = (0, 0, 0)´

→ Relationship between the frames my_base_link and my_base_scan:

• Translation, t = (x, y, z)´ = (-0.09, 0, 0.114)´

• Rotation, r = (roll, pitch, yaw)´ = (0, 0, 0)´

Visualize the tf tree in Rviz:

$ ros2 launch myrobottf turtlebot3_tf.launch.py

$ ros2 run rviz2 rviz2

• Click the Add button and choose TF, to visualize the tf information.

Hint

Switch your fixed_frame in RVIZ to the start frame of your tf tree, that is right now, base_footprint.

→ You should see the different coordinate frames of your Turtlebot3, based on your static transforms.

Creating a Dynamic Transform

Dynamic transforms are variant transformations, which change over time. The convenient way is to use the Python API to define frame relationships.

Dynamic TF Exercise

Write a transform Broadcaster and define a dynamic relationship between the frames odom and base_footprint. Therefore, create a node named simulated_odom.py in the package myrobottf. By providing changes in the translation values x and y, the turtlebot takes a simulated path. Use the following mathematical definition and the Python code example.

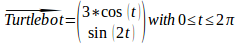
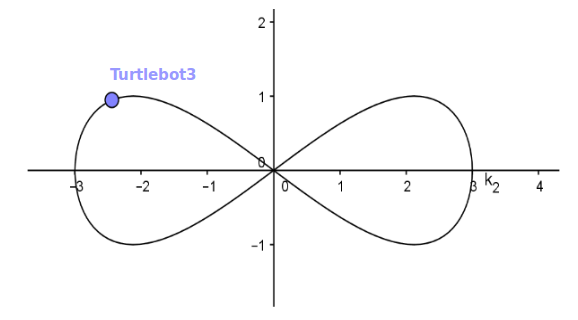
Figure 7 Image 1. Virtual Turtlebot Path

Listing 14 simulated_odom.py

#!/usr/bin/env python3

import rclpy
import tf2_ros

import scipy
import numpy
from geometry_msgs.msg import TransformStamped

from scipy.spatial.transform import Rotation

cnt = 0

def calculate_position():
    global cnt
    if cnt > 300:
        cnt = 0
    cnt = cnt+1
    x = 3* numpy.cos(cnt*0.02)
    y = numpy.sin(2*cnt*0.02)

    position = (x,y)
    return position

def calculate_tf():
    global mydynamictf
    t = TransformStamped()
    #getting actual position
    position_turtlebot = calculate_position()
    #calculating transform
    now = mydynamictf.get_clock().now().to_msg()
    t.header.stamp = now
    t.header.frame_id = "odom"
    t.child_frame_id = "base_footprint"
    t.transform.translation.x = position_turtlebot[0]
    t.transform.translation.y = position_turtlebot[1]
    t.transform.translation.z = 0.0
    euler = Rotation.from_euler('zyx', [0.0, 0.0, 0.0])
    quat = euler.as_quat()
    t.transform.rotation.x = quat[0]
    t.transform.rotation.y = quat[1]
    t.transform.rotation.z = quat[2]
    t.transform.rotation.w = quat[3]
    return t

def mytimercallback():
    global mydynamictf
    odom_to_base_footprint = calculate_tf()
    br = tf2_ros.transform_broadcaster.TransformBroadcaster(mydynamictf)
    br.sendTransform(odom_to_base_footprint)

def main():
    global mydynamictf
    rclpy.init()
    mydynamictf = rclpy.create_node('my_dynamic_tf')
    mydynamictf.create_timer(1.0 / 30.0, mytimercallback)
    try:
        rclpy.spin(mydynamictf)
    except KeyboardInterrupt:
        pass    
    mydynamictf.destroy_node()
    rclpy.shutdown()

if __name__ == '__main__':
    main()

To simplify the transformation from euler to quaternion we are using a scipy function. For that purpose we need to install the scipy library:

$ pip3 install scipy

Explanation

The basic structure of a simple node is already well known. So, only the tf specific lines will be explained.

import tf2_ros

These lines import the essential TF modules. The tf2_ros package provides ROS2 bindings to tf2.

Create an object br of the TransformBroadcaster class:

    br = tf2_ros.transform_broadcaster.TransformBroadcaster(mydynamictf)

This will initialize a ROS2 TF2 Broadcaster, which allows to send transforms from one frame to another one.

    odom_to_base_footprint = calculate_tf()

Calculates the transform from base_footprint to odom

    position = (x,y)

Returns the virtual x and y position of the turtlebot.

    br.sendTransform(odom_to_base_footprint)

The handler function sendTransform() for the turtlebot pose broadcasts the turtlebot’s translation and rotation, and publishes it as a transform from frame odom to frame base_footprint.

The sendTransform function is from the message type TransformStamped, which was set up in the calculate_tf definition:

• Header

• Child Frame ID (Frame ID to which the transform is happening)

• Transform

Exercise

Run your node and visualize the dynamic tf tree in Rviz.